PyTorch の自動微分 (torch.autograd)

torch.autograd provides classes and functions implementing automatic differentiation of arbitrary scalar valued functions. *1

PyTorch のドキュメントを読んでもよく分からなかったので，こちらのサンプルを参考にしました．

任意の関数の勾配を自動的に計算してくれるらしいのですが，最初は手動でやらないと何をしてくれているのか分からないので，torch.autograd を使わずに，最小二乗法のようなものを機械学習で実装してみます．

データの準備

傾きa，y切片bの直線について，区間 [-10, 10] の値に少し乱数を加えたものを (x, y) と定義します．これらの回帰直線を最小二乗法を用いて傾きta，y切片tbを導出します．

import numpy as np
import torch
import matplotlib.pyplot as plt

n = 10
a = 2
b = -4

x = np.arange(-n, n + 1, 1)
y = a * x + b + np.random.randn(2 * n + 1)

data = torch.tensor(np.vstack((x, y)), dtype=torch.float32)


def reg(x, y):
    a = np.cov(x, y)[0][1] / np.var(x)
    b = np.mean(y) - a * np.mean(x)
    return a, b


ta, tb = reg(x, y)
ty = ta * x + tb

plt.title("data")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim(-12, 12)
plt.ylim(-25, 25)
plt.grid(True, which="both")
plt.plot(x, ty)
plt.plot(x, y, "o")
plt.text(0, -10, rf"$y = {ta:.3f} x {tb:.3f}$")
plt.savefig("data.png")

torch.save(data, "data.pt")

データをグラフにしました．

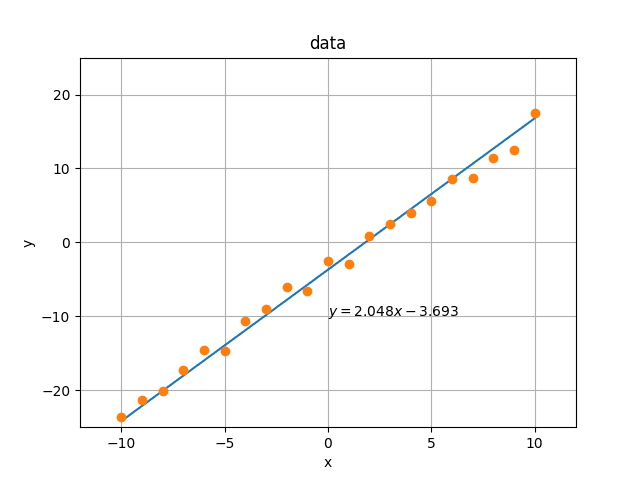
(x, y) の情報から，機械学習手法を用いて，回帰直線の傾きtaとy切片tbを計算し，上記の結果に一致するかを確認します．

勾配を求める関数を手動で作る

こちらのサンプルを参考にしました．損失関数は平均二乗誤差を用いました．

import os

import torch
from torch.utils.tensorboard import SummaryWriter

def model(x, w, b):
    return w * x + b


def loss_fn(p, y):
    return ((p - y) ** 2).mean()  # mean squared error


def dloss_fn(p, y):
    return 2 * (p - y) / p.size(0)


def dmodel_dw(x, _w, _b):
    return x


def dmodel_db(_x, _w, _b):
    return 1.0


def grad_fn(x, y, p, w, b):
    dloss_dtp = dloss_fn(p, y)
    dloss_dw = dloss_dtp * dmodel_dw(x, w, b)
    dloss_db = dloss_dtp * dmodel_db(x, w, b)
    return torch.stack([dloss_dw.sum(), dloss_db.sum()])

学習させます．

def train(epoch, learning_rate, params, x, y):
    with SummaryWriter() as writer:
        for i in range(epoch):
            w, b = params
            p = model(x, w, b)
            loss = loss_fn(p, y)
            grad = grad_fn(x, y, p, w, b)
            params -= learning_rate * grad
            writer.add_scalar("loss", loss, i)
            if i % 100 == 0:
                print("Epoch %d, Loss %f" % (i, float(loss)))
        return params

def main():
    data = torch.load(os.path.join(base_dir, "data.pt"))
    x = data[0, :]
    y = data[1, :]
    params_w, params_b = train(
        epoch=2001,
        learning_rate=1e-3,
        params=torch.tensor([1.0, 0.0]),
        x=x,
        y=y,
    )
    print(f"params_w={params_w:.3f}, params_b={params_b:.3f}")

実行し，以下の結果を得ました．

Epoch 0, Loss 47.608883
Epoch 100, Loss 10.011012
Epoch 200, Loss 6.996218
Epoch 300, Loss 4.976156
Epoch 400, Loss 3.622606
Epoch 500, Loss 2.715659
Epoch 600, Loss 2.107960
Epoch 700, Loss 1.700769
Epoch 800, Loss 1.427933
Epoch 900, Loss 1.245117
Epoch 1000, Loss 1.122620
Epoch 1100, Loss 1.040541
Epoch 1200, Loss 0.985544
Epoch 1300, Loss 0.948694
Epoch 1400, Loss 0.924002
Epoch 1500, Loss 0.907456
Epoch 1600, Loss 0.896371
Epoch 1700, Loss 0.888943
Epoch 1800, Loss 0.883966
Epoch 1900, Loss 0.880630
Epoch 2000, Loss 0.878396
params_w=1.950, params_b=-3.626

いい感じに学習できました．

`torch.autograd` を使う

自動微分を使って書き換えます．こちらのサンプルを参考にしました．モデルと損失関数は共通です．

def train(epoch, learning_rate, params, x, y):
    with SummaryWriter() as writer:
        for i in range(epoch):
            if params.grad is not None:
                params.grad.zero_() # 1
            p = model(x, *params)
            loss = loss_fn(p, y)
            loss.backward() # 2
            with torch.no_grad():
                params -= learning_rate * params.grad # 3
            writer.add_scalar("loss", loss, i)
            if i % 100 == 0:
                print("Epoch %d, Loss %f" % (i, float(loss)))
        return params

def main():
    data = torch.load(os.path.join(base_dir, "data.pt"))
    x = data[0, :]
    y = data[1, :]
    params_w, params_b = train(
        epoch=2001,
        learning_rate=1e-3,
        params=torch.tensor([1.0, 0.0], requires_grad=True), # 4
        x=x,
        y=y,
    )
    print(f"params_w={params_w:.3f}, params_b={params_b:.3f}")

params の勾配を初期化し，2. loss テンソル (tensor(47.6089, grad_fn=<MeanBackward0>))の .backward() 関数を呼び，3. torch.no_grad() の中でパラメータを調整します．また，4. requires_grad を有効にします．

実行したところ，全く同じ結果が得られました．手動で作成した grad_fn() 関数を使わずに同じ計算ができていることが確認できました．

...
params_w=1.950, params_b=-3.626

Optimizer を使う

torch.optim.SGD を利用して更に簡単に計算してみます *2．このサンプルを参考にしました．

def train(epoch, learning_rate, params, x, y):
    optimizer = torch.optim.SGD([params], lr=learning_rate) # 1
    with SummaryWriter() as writer:
        for i in range(epoch):
            p = model(x, *params)
            loss = loss_fn(p, y)
            optimizer.zero_grad() #2
            loss.backward()
            optimizer.step() #3
            writer.add_scalar("loss", loss, i)
            if i % 100 == 0:
                print("Epoch %d, Loss %f" % (i, float(loss)))
        return params


def main():
    data = torch.load(os.path.join(base_dir, "data.pt"))
    x = data[0, :]
    y = data[1, :]
    params_w, params_b = train(
        epoch=401,
        learning_rate=1e-2,
        params=torch.tensor([1.0, 0.0], requires_grad=True),
        x=x,
        y=y,
    )
    print(f"params_w={params_w:.3f}, params_b={params_b:.3f}")

optimizer を初期化し，2. 勾配を初期化してから，3. 計算します．学習させました．

Epoch 0, Loss 47.608883
Epoch 100, Loss 1.113696
Epoch 200, Loss 0.878076
Epoch 300, Loss 0.873932
Epoch 400, Loss 0.873859
params_w=1.950, params_b=-3.692