PyTorch で時系列データを学習させてみたかったので,このサンプルを参考に,long short-term memory (LSTM) cell を使った,Recurrent neural network を作成し,ある区間の sin 関数を学習させて,その続きを予測させてみました.
sin 関数は,振幅と周波数と位相の3個のパラメータがありますが,参考にしたサンプルは位相のみを変化させた学習データを用いていました.もう少し凝った学習ができるのか興味があったので,振幅も変化させることにしました.
教師データの作成
import numpy as np import torch np.random.seed(2) T = 40 L = 1000 N = 100 x = np.empty((N, L), "int64") x[:] = np.array(range(L)) + np.random.randint(-4 * T, 4 * T, N).reshape(N, 1) data = (np.random.rand(N, 1) * np.sin(x * 1.0 / T)).astype("float64") torch.save(data, "data.pt")
np.array(range(L)) で位相をずらしています.np.random.rand(N, 1) で振幅をランダムに指定し,np.sin(x * 1.0 / T) で一定の周波数を指定し,これらを掛け算してデータを生成します.
作成した100個 (N) のデータのうち,最初の3個をテスト用に,残りの97個を学習に使用することにします.テスト用データは下の図のように,周波数のみが一致した sin 関数になっていることを確認しました.

学習と予測
モデルは以下のようにしました.ほとんど参考にしたサンプルと同じです.
import torch import torch.nn as nn import torch.optim as optim import numpy as np from torch.utils.tensorboard import SummaryWriter class Sequence(nn.Module): n: int def __init__(self, n=16) -> None: super().__init__() self.n = n self.lstm1 = nn.LSTMCell(1, self.n) self.lstm2 = nn.LSTMCell(self.n, self.n) self.linear = nn.Linear(self.n, 1) def forward(self, input, future=0): outputs = [] h_t = torch.zeros(input.size(0), self.n, dtype=torch.double) c_t = torch.zeros(input.size(0), self.n, dtype=torch.double) h_t2 = torch.zeros(input.size(0), self.n, dtype=torch.double) c_t2 = torch.zeros(input.size(0), self.n, dtype=torch.double) for input_t in input.split(1, dim=1): h_t, c_t = self.lstm1(input_t, (h_t, c_t)) h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2)) output = self.linear(h_t2) outputs += [output] for _ in range(future): h_t, c_t = self.lstm1(output, (h_t, c_t)) h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2)) output = self.linear(h_t2) outputs += [output] outputs = torch.cat(outputs, dim=1) return outputs
このモデルを学習させました.
def train(steps: int, future=1000): np.random.seed(0) torch.manual_seed(0) # data = torch.load("data.pt") input = torch.from_numpy(data[3:, :-1]) target = torch.from_numpy(data[3:, 1:]) test_input = torch.from_numpy(data[:3, :-1]) test_target = torch.from_numpy(data[:3, 1:]) # draw_data(test_input, future) # seq = Sequence(32) seq.double() criterion = nn.MSELoss() optimizer = optim.LBFGS(seq.parameters(), lr=0.8, tolerance_grad=1e-9) # with SummaryWriter() as writer: for i in range(steps): print(f"STEP: {i}") def closure(): optimizer.zero_grad() out = seq(input) loss = criterion(out, target) print("loss:", loss.item()) writer.add_scalar("train-loss", loss.item(), i) loss.backward() return loss optimizer.step(closure) # begin to predict, no need to track gradient here with torch.no_grad(): pred = seq(test_input, future) loss = criterion(pred[:, :-future], test_target) print("test loss:", loss.item()) writer.add_scalar("test-loss", loss, i) draw(input, future, pred.detach().numpy(), i)
optimizer は L-BFGS algorithm を使用し,loss function は mean squared error を使用しました.
train-loss
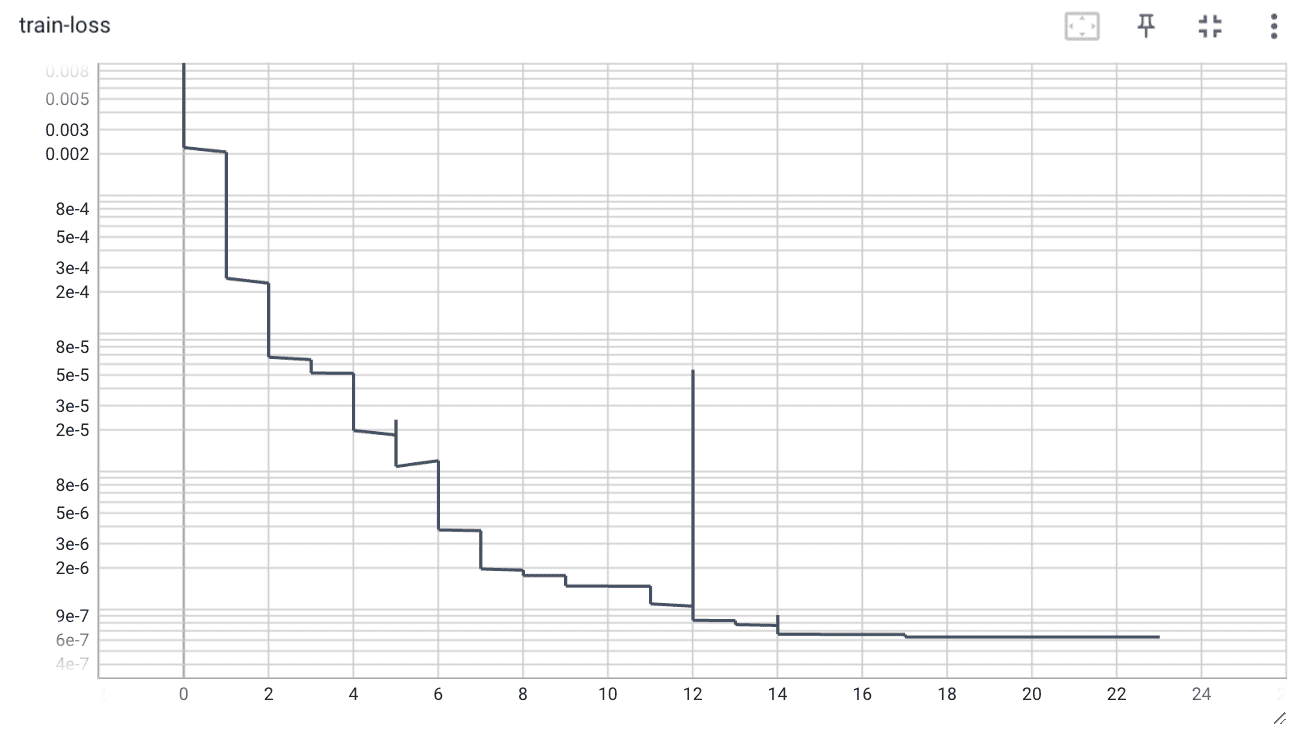
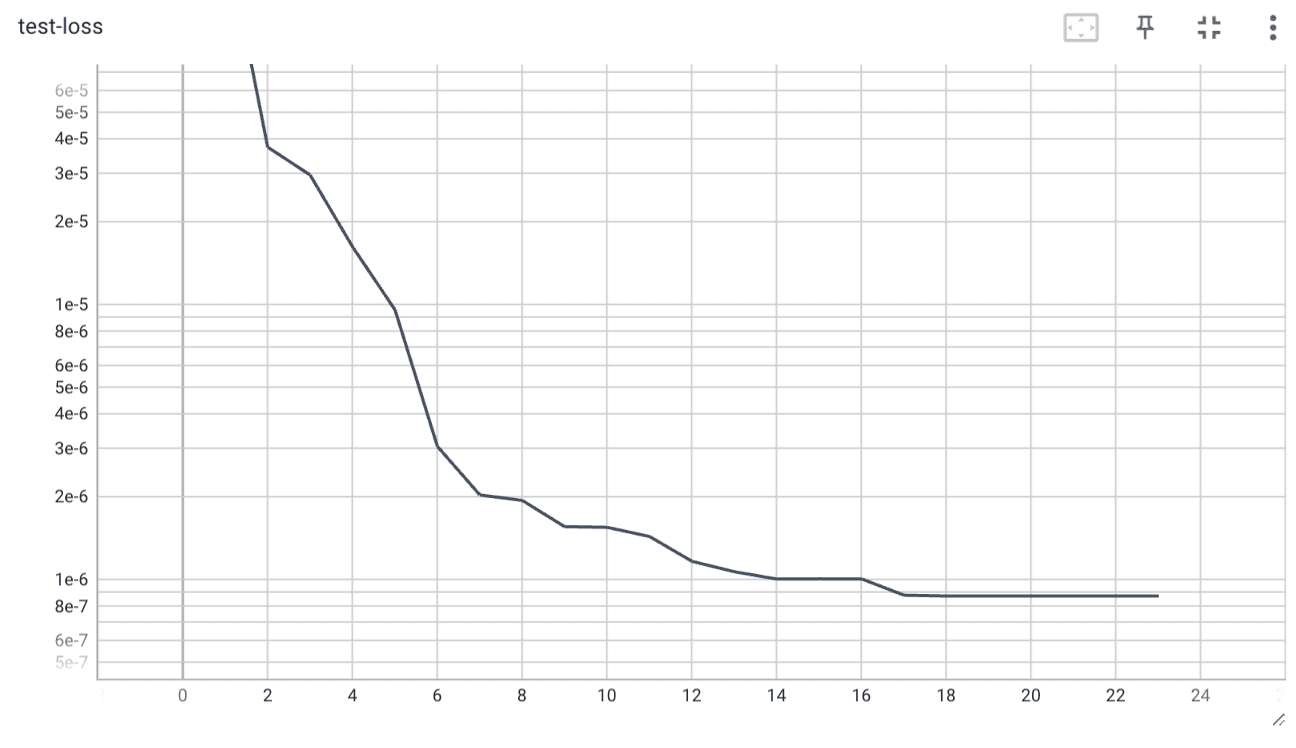
test-loss
過学習は見られませんでした.
予測結果
学習の途中で予測結果を出力してグラフにしました.step=6ぐらいから周期性が出現し,step=12ぐらいから振幅が整い始めました.








いい感じに予測ができるようになっていることが分かりました.
まとめ
sin 関数を学習させる記事を 2015 年に公開しましたが,PyTorch のおかげでより高いレベルの予測ができるようになったので満足しました.