Pythonで生存分析

Pythonで生存分析の練習をしながら統計の理解を深めるための記事です．この記事を読めば，統計のreview論文1つとPythonを用いた統計処理が追えるようになっています．

Critical Care 2004, 8:389-394に書いてあることを適宜訳しながらPythonで検証します．

環境

Python 3.7.4
jupyterlab 1.2.6
lifelines 0.24.1 (conda-forge)
pandas 1.0.1

イントロダクション

生存期間 (survival time) は，フォローアップを開始してから決められたイベントが発生するまでの期間を計測したデータである．例えば，寛解となってから非寛解となるまでの期間や，病気が診断されてから死亡するまでの期間である．このようなデータを扱うのに，標準的な統計技術は使用することができない．なぜならば，母集団の分散(distribution)が通常とは異なり，打ち切り(censored)が発生するからである．フォローアップ期間において，イベントが発生していない，または発生したことが分からない場合を，打ち切りという．例えば，寛解期間の研究において，研究終了時点で患者が寛解の状態の場合，患者の寛解期間は打ち切られる．患者が何らかの理由で研究期間中に追跡できなくなった場合，患者のフォローアップ期間は打ち切られたと解釈される．

架空のデータをTable 1に示した．このレビューではこのデータを使って，実際に統計処理の方法を解説する．このデータにおいて，イベントは患者の死亡(death)と定義されており，打ち切りとは，生存(survival)か不明(unknown)のことを意味する．

import pandas as pd
df = pd.read_csv("data.csv")
df

index	time	outcome	treatment	age
0	1	Died	2	75
1	1	Died	2	79
2	4	Died	2	85
3	5	Died	2	76
4	6	Unknown	2	66
5	8	Died	1	75
6	9	Survived	2	72
7	9	Died	2	70
8	12	Died	1	71
9	15	Unknown	1	73
10	22	Died	2	66
11	25	Survived	1	73
12	37	Died	1	68
13	55	Died	1	59
14	72	Survived	1	61

カプランマイヤー法を用いた生存曲線の推定

生存の解析において，生存関数(survival function)とハザード関数(hazard function)，この2つの関数は時間に依存しないため重要である．生存関数 $S(t)$ は，少なくとも時刻 $t$ までに生存している確率である．ハザード関数 $h(t)$ は，時刻 $t$ で生存している人が死亡する条件付き確率である．時間 $t$ と生存関数 $S(t)$ のグラフと生存曲線(survival curve)という．カプランマイヤー(Kaplan–Meier)法を用いることで，確率分布を計算しなくても生存曲線を推定することができる．カプランマイヤー法は以下の累積生存率の式を用いる．

$S(k) = p_1 \cdot p_2 \cdot p_3 \cdot \ldots \cdot p_k$

$p_k$ は期間 $k$ における生存率であり，

$p_i =\frac {r_i - d_i} {r_i}$

$r_i$ は期間 $i$ の最初に生存していた人数で， $d_i$ はこの期間で死亡した人数である．

Table 1の治療2を受けた患者のデータを用いて，Table 2のような計算をすると，Figure 1が得られる．

dfs = pd.get_dummies(df,["outcome"])

index	time	treatment	age	outcome_Died	outcome_Survived	outcome_Unknown
0	1	2	75	1	0	0
1	1	2	79	1	0	0
2	4	2	85	1	0	0
3	5	2	76	1	0	0
4	6	2	66	0	0	1
5	8	1	75	1	0	0
6	9	2	72	0	1	0
7	9	2	70	1	0	0
8	12	1	71	1	0	0
9	15	1	73	0	0	1
10	22	2	66	1	0	0
11	25	1	73	0	1	0
12	37	1	68	1	0	0
13	55	1	59	1	0	0
14	72	1	61	0	1	0

from lifelines.plotting import plot_lifetimes
ax = plot_lifetimes(dfs["time"], event_observed=dfs["outcome_Died"])
ax.set_xlabel("time [days]")
ax.set_ylabel("patient number")

plotting — lifelines 0.24.2 documentation

f:id:atsuhiro-me:20200319182726p:plain:w320

from lifelines import KaplanMeierFitter
_, td = list(dfs.groupby("treatment"))[1]
kmf = KaplanMeierFitter()
kmf.fit(td["time"], td["outcome_Died"],label="treatment 2")
ax = kmf.plot(show_censors=True)
ax.set_xlabel("survival time [days]")
ax.set_ylabel("probability of survival")

KaplanMeierFitter — lifelines 0.24.2 documentation

index	time	treatment	age	outcome_Died	outcome_Survived	outcome_Unknown
0	1	2	75	1	0	0
1	1	2	79	1	0	0
2	4	2	85	1	0	0
3	5	2	76	1	0	0
4	6	2	66	0	0	1
6	9	2	72	0	1	0
7	9	2	70	1	0	0
10	22	2	66	1	0	0

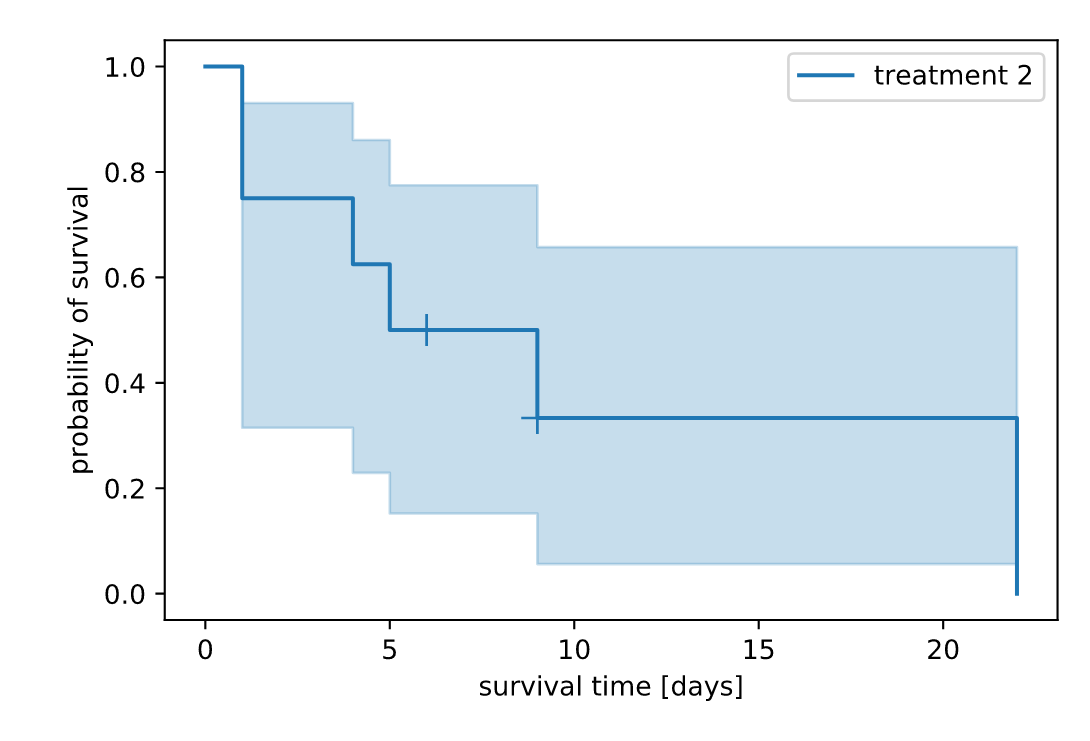f:id:atsuhiro-me:20200319182949p:plain:w320 Figure 1

2つの治療法を比較すると，Figure 2のようになる．

from lifelines import KaplanMeierFitter
for name, td in dfs.groupby("treatment"):
    kmf = KaplanMeierFitter()
    kmf.fit(td["time"], td["outcome_Died"],label=f"treatment {name}")
    ax = kmf.plot(show_censors=True)
ax.set_xlabel("survival time [days]")
ax.set_ylabel("probability of survival")
ax.axhline(y=0.5, xmin=0, xmax=1, linestyle=":", color="k")

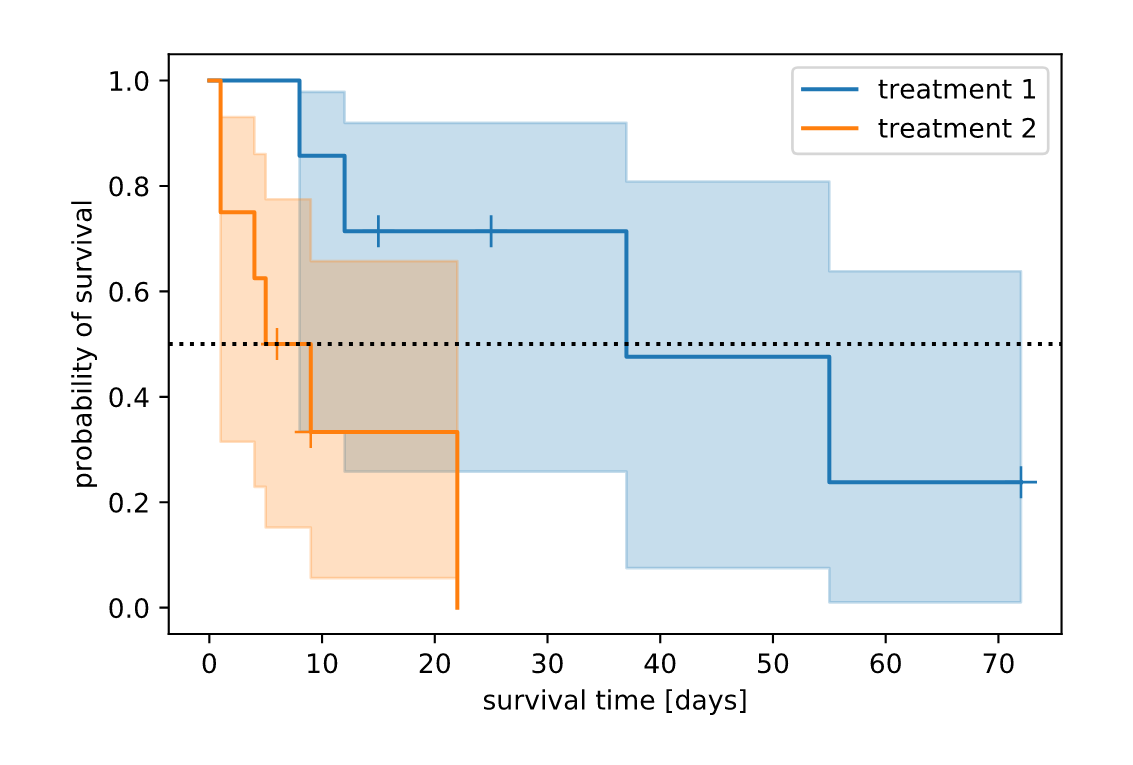f:id:atsuhiro-me:20200319191428p:plain:w320 Figure 2

このグラフから，治療2よりも治療1の方が生存率が高いように思われる．カプランマイヤー曲線を使用すると，50％生存期間 (median survival time) *1を推定することができる．グラフの0.5の横線の値から，この治療の50％生存期間は，治療1が37日，治療2が5日であることが分かる．

ログランク検定を用いた2群間の生存曲線の検定

2群間の生存曲線の比較をするには，ログランク検定 (log rank test) という統計的な仮説検定 (hypothesis test) を行う．2群間の生存曲線に差がない，すなわち，すべての時点においてイベントが発生する確率は等しい，という帰無仮説 (null hypothesis ) を検定する．検定統計量 (test statistic) は以下の式で定義される．

${\chi^2} \mathrm {(log rank)} = \frac {(O_1-E_1)^2} {E_1} + \frac {(O_2-E_2)^2} {E_2}$

$O_1$ と $O_2$ は群1と群2における発生したイベントの合計数 (total numbers of observed events) であり， $E_1$ と $E_2$ は予想されるイベントの合計数 (total numbers of expected events) である．

予想されるイベントの合計数は，それぞれの時刻における予想イベント数 (expected number of events) の合計である．ある時刻における予想イベント数は，その時刻の死亡リスクと生存数をかけ合わせたものである．帰無仮説において，死亡リスクは2群を合わせたデータから計算される．検定統計量を自由度が1のχ2分布と比較して計算する．Table 3に実際の計算を示した．

from lifelines.statistics import multivariate_logrank_test
r = multivariate_logrank_test(dfs["time"],dfs["treatment"],dfs["outcome_Died"])
r.print_summary()

statistics — lifelines 0.24.2 documentation

t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
test_name = multivariate_logrank_test
test_statistic = 5.68
p = 0.02

P値が十分小さいため，2群間の生存曲線に統計的有意差があることが示された．

コックス比例ハザードモデルを用いた2群間の生存曲線の検定

ログランク検定は2群間の生存期間に有意差があるかを検定するために使われるが，他の説明変数を考慮することはできない．

コックス比例ハザードモデル (Cox’s proportional hazards model) を用いることで，複数の群における生存曲線の差を推定する時に，他の因子を検定することができる．このモデルにおいて，「ハザード」が重要である．ハザードとは，死亡する確率，ないしは研究対象のイベントが発生する確率のことである．

コックス比例ハザードモデルでは，ハザードの確率分布を仮定する必要はない．ただし，ある時点において死亡する確率は，片方の群がもう片方の群の2倍高いとすると，すべての時点において2倍高いという仮定をする．つまり，ハザード比 (hazard ratio) は時間に依存しないと仮定する．

これを用いてTable 1のデータをコックス比例ハザードモデルで解析する．

from lifelines import CoxPHFitter
dft = pd.get_dummies(df,columns=["treatment"],drop_first=True)
dft["outcome"] = dft["outcome"].map({"Died":1, "Survived":0,"Unknown":0})
cph = CoxPHFitter()
cph.fit(dft, "time","outcome")
cph.print_summary()
ax = cph.plot()
ax.set_ylim(-0.5, 1.5)
ax.set_xlim(-5, 5)

CoxPHFitter — lifelines 0.24.2 documentation

model = lifelines.CoxPHFitter
duration col = 'time'
event col = 'outcome'
baseline estimation = breslow
number of observations = 15
number of events observed = 10
partial log-likelihood = -13.04

	coef	exp(coef)	se(coef)	coef 95%	exp(coef) 95%	z	p	-log2(p)
age	0.22	1.24	0.08	0.05-0.38	1.05-1.47	2.58	0.01	6.66
treatment_2	1.88	6.59	0.97	-0.01-3.78	0.99-43.93	1.95	0.05	4.28

f:id:atsuhiro-me:20200320022215p:plain:w320

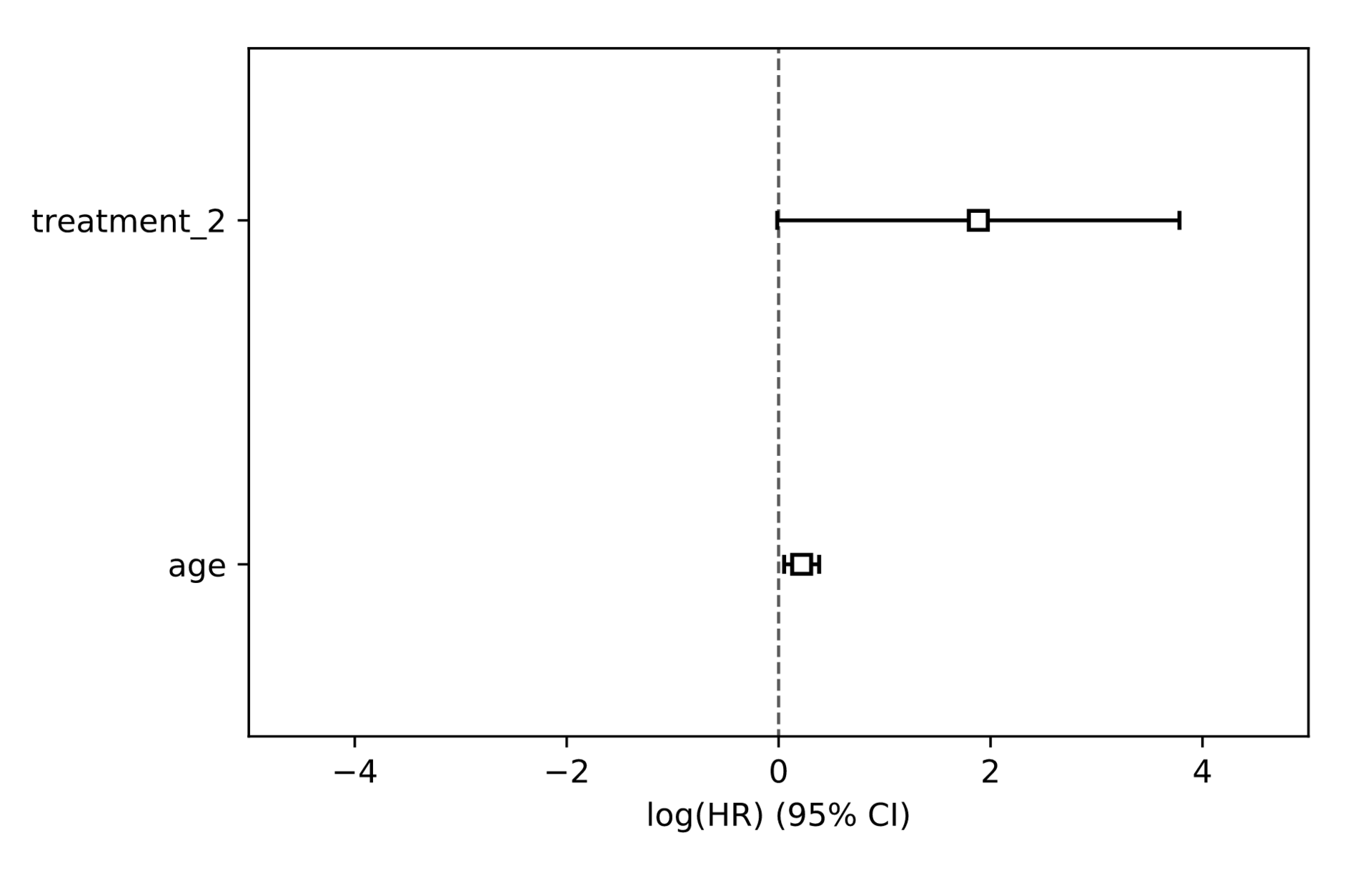
P値によると，治療の影響は統計的に有意差と断言できないが，年齢は有意に影響があると言える．治療のexp(coef) 95%が1を含むことから，治療が異なる2群には有意差がないのかもしれない．

年齢のexp(coef)が1.24であることから，ある患者が別の患者よりも1歳年上で，2人とも同じ治療を受けたとしたら，死亡する確率が1.24倍高いと言える．exp(coef) 95%が1を含まないことから，年齢という因子は統計的に有意に異なるといえる．

文献の例

Chest. 2004 May;125(5):1815-20.では，気管支拡張症の患者の生存期間を，年齢と長期酸素療法の有無で解析している．カプランマイヤー曲線とログランク検定の結果がFigure 4に示す．生存曲線は有意に異なることが分かる．

この研究では，コックス比例ハザードモデルを用いて解析し，Table 6のような結果となった．年齢と長期酸素療法の有無は，生存期間において有意差があることが示された．

前提と制限

ログランク検定と，コックス比例ハザードモデルでは，ハザード比が常に一定であると仮定している．使用する時は，この前提が成り立っているのか確認する必要がある．

結論

生存解析を行うことで，治療が異なる複数の群における死亡確率や他のイベントの確率を解析することができる．生存期間を測定するには，開始時点と終了時点を明確に定義するべきであり，打ち切りが発生したことと記録するべきである．この論文では，特に頻繁に使用される方法について述べた．カプランマイヤー方法で，生存曲線を推定する．ログランク検定で，2群間の生存期間の差を統計的に検定する．コックス比例ハザードモデルで，別の共変量を考慮することができる．ログランク検定とコックス比例ハザードモデルはハザード比が常に一定であると仮定する．

みーのまとめ

実際のデータを使いながら検定を行うことで，統計の理解が深まりました．上記論文のデータは，ログランク検定で有意差が出ているのに，コックス比例ハザードモデルでは有意差が出ないという結論でした．検定方法によって結果が変わることにも注意するべきです．

*1:median survival timeは長らく「生存期間中央値」と訳されてきたが，このmedianは中央値という統計的な意味ではなく，半分の，という意味であるため，ホーム｜造血器腫瘍診療ガイドライン 2018年版｜一般社団法人日本血液学会などのガイドラインを参照すると，最近は「50％生存期間」と訳されるようになってきている．

みーのぺーじ

みーが趣味でやっているPCやソフトウェアについて．Python, Javascript, Processing, Unityなど．

環境

目次